INTRODUCTION
The human cervical spine, a complex structure responsible for supporting and facilitating the movement of the head, is susceptible to degenerative changes due to repetitive motions and extended postures required for daily activities.1 These degenerative alterations are particularly pronounced in cases of non-specific chronic neck pain (NSCNP).1,2 It is widely accepted that deviations in alignment and movement patterns can trigger the onset of painful and degenerative conditions in the cervical spine.2
Cervical protraction and retraction, representing a com-bination of upper cervical extension and lower cervical flexion, play pivotal roles in cervical spine motion. Previous research has measured total head excursion, encompassing cervical protraction and retraction, as a sagittal translational motion in centimeters.3-6 Notably, individuals with neck pain exhibited distinct patterns, with a 7.5 cm total head excursion compared to 10.9 cm in healthy individuals.3 Moreover, retraction displayed a significantly greater range in the neck pain group.4 Cervical protraction and retraction have also been quantified as craniovertebral angles (CVAs) in healthy individuals.7 Given the ubiquity of cervical protraction in everyday activities and the therapeutic use of retraction to address neck pain, these movements present as valuable variables for classifying neck pain. Thus, it is reasonable to suspect a correlation among cervical protraction, retraction, and neck pain. However, despite the growing emphasis on proper movement, motor control, and coordination,8-11 it remains uncertain whether upper and lower cervical movements during cervical protraction and retraction differ between individuals with and without neck pain. Additionally, quantitative assessments of these kinematics in individuals with neck pain during cervical protraction and retraction are conspicuously absent from existing literature.
Previous studies investigating the linear relationship be-tween neck pain and movement have produced inconsistent results, possibly indicative of a nonlinear relationship.3,12 Traditional methods such as linear and logistic regression may be ill-suited to capture such nonlinear relationships.13 In response, machine learning (ML) approaches are being increasingly adopted for classification tasks. The strength of ML lies in its ability to model both linear and highly nonlinear relationships, potentially yielding superior accuracy compared with conventional statistical methods.13
Consequently, this study aimed to achieve two primary objectives: 1) to develop, assess, and compare the predictive performance of statistical ML models for classifying individuals with and without NSCNP using cervical movements during protraction and retraction and 2) to investigate the association between cervical movements and NSCNP.
METHODS
A total of 277 public service office workers (POWs) who did not have NSCNP and 463 POWs with NSCNP were carefully screened for eligibility. The inclusion criteria were that POWs had been employed in office settings, used computers for more than two years, and were recruited between September 2022 and March 2023. The eligibility criteria for individuals with NSCNP included two main factors: (1) they had to report an average neck pain intensity rating exceeding 3 out of 10 on a Numerical Rating Scale (NRS) for the preceding four weeks,14 and (2) neck pain intensity rating exceeding 2 out of 4 on the Northwick Park Neck Pain Questionnaire (NPQ).15 Asymptomatic individuals were eligible if they had not experienced neck pain that warranted treatment from a healthcare professional within the past two years. Exclusion criteria for both POWs, with or without NSCNP, encompassed a history of prior spinal surgery, rheumatologic conditions, ongoing or chronic respiratory conditions, or active compensation claims related to injuries. To conduct a statistical analysis of the impact of NSCNP involving up to eight variables, a sample size of no less than 80 participants was deemed necessary in accordance with the common rule of using one variable per 10 events.13 The data utilized in this study were derived from musculoskeletal screening tests conducted to prevent industrial accidents among POWs. These data were collected from April 2022 to February 2023, with a focus on examining the risk factors associated with musculoskeletal disorders in public service offices. It is important to note that for this study, informed consent was waived by the Yonsei University Mirae Campus Institutional Review Board prior to the commencement of data queries and analyses (IRB number:1041849-202306-BM-100-01). This waiver was granted because the study involved the analysis of preexisting data collected during the assessment of musculoskeletal disorder risk factors.
We tracked the markers to estimate cervical movements during protraction and retraction. This tracking was accomplished using Python (Version 3.6.15; Python Software Foundation) with the primary computer vision library OpenCV. The tracking algorithm employed was the Channel and Spatial Reliability Tracking tracker, known for its reliability and robustness in tracking.16,17
For video recording, we used a Samsung Galaxy S20 smartphone (Samsung Inc., Seoul, Korea) equipped with a 4 K video recording application, capturing video at a resolution of 3,840×2,160 pixels at 60 frames per second. The smartphone was securely mounted on a tripod, positioned 100 cm from the side of the chair, and adjusted to the height corresponding to the level of the subject's tragus. To facilitate tracking, two spherical markers, each with a diameter of 20 mm, were affixed to the tragus of the ear and spinous process of C7.
The head tilt angle (HTA) was calculated as the angle formed between the line connecting the lateral canthus of the eye, a marker on the tragus of the ear, and a vertical line passing through the midpoint of the tragus marker (canthus-tragus-horizontal) (Figure 1).11,18 The CVA was measured between the line connecting the two markers on the tragus of the ear and the spinous process of C7 and a horizontal line passing through the marker on the spinous process of C7 (Figure 1).11,18 The head excursion angle (HEA) was determined by combining HTA and CVA measurements. HEA was defined as the angle between the line connecting the two markers on the tragus of the ear and the spinous process of C7, and the line connecting the lateral canthus of the eye to the marker on the tragus of the ear (Figure 1).19 Protraction and retraction distances were assessed by measuring the displacement of the marker on the tragus between the initial resting position and the endpoints of cervical protraction and retraction (Figure 1).
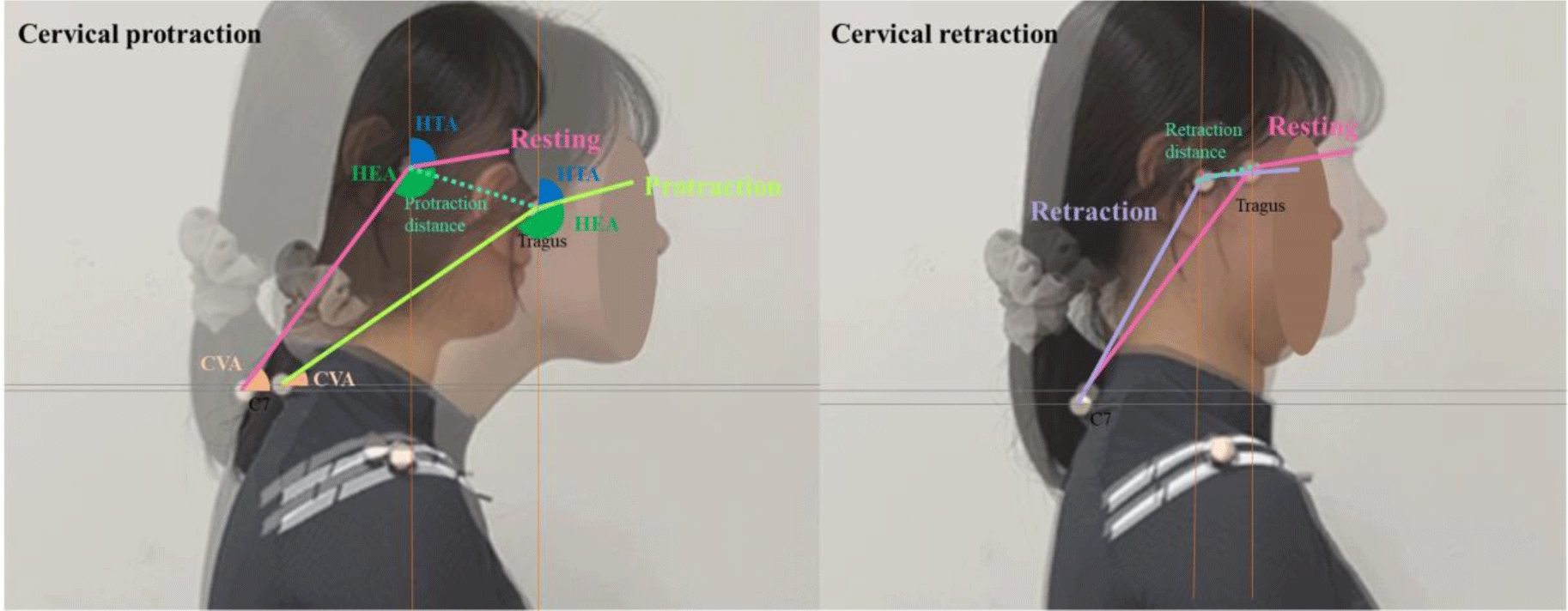
For cervical movements during retraction, the partici-pants were instructed to retract their heads as much as possible and then return to the starting position. Pro- and retraction were performed consecutively, and each proce-dure was repeated three times.
The head tilt, craniovertebral, and head excursion angles during protraction and retraction were measured while the subjects were in a seated position. For cervical movement analysis during protraction and retraction, measurements included HTA, CVA, HEA, and protraction and retraction distances at the endpoints of cervical protraction and retraction. The endpoints of protraction and retraction were defined as the positions where the most significant movement occurred in a positive or negative direction from the typical seated posture along the horizontal axis. We subtracted the HTA, CVA, and HEA at the endpoints of protraction and retraction from the HTA, CVA, and HEA in the resting position to quantify the movement of the upper and lower cervical spine.
HTA during protraction (PHTA)=HTA in end point of protraction – HTA in resting
CVA during protraction (PCVA)=CVA in resting – CVA in end point of protraction
HEA during protraction (PHEA)=HEA in end point of protraction – HEA in resting
HTA during retraction (RHTA)=HTA in end point of retraction – HTA in resting
CVA during retraction (RCVA)=CVA in resting – CVA in end point of retraction
HEA during retraction (RHEA)=HEA in end point of retraction – HEA in resting
As PHTA becomes less pronounced (more negative), the upper cervical extension increases during protraction. With increasing PCVA (greater positive values), the lower cervical flexion also increased during protraction. As the PHEA gains strength (more positive values), cervical protraction becomes more pronounced during this movement. With a growing RHTA (increasing positive values), upper cervical flexion intensifies during retraction. Conversely, a decrease in RCVA (more negative values) resulted in a greater lower cervical extension during retraction. Decreasing the RHEA (more negative values) leads to increased cervical retraction during this phase.
We conducted ML analysis using Orange data mining software (Version 3.3.0, developed in Ljubljana, Slovenia) in conjunction with Python (Version 3.6.15, developed by the Python Software Foundation).
Eight numerical predictors (PHTA, PCVA, PHEA, RHTA, RCVA, RHEA, protraction, and retraction distances) were included in the present study. The target was transformed into a dichotomous variable with and without NSCNP. Exploratory data analysis was performed to detect missing data. Imputation for handling missing data was performed by eliminating instances with unknown values. We assessed the distribution of each variable using various visualization methods, including boxplots, scatterplots, and linear projections. This comprehensive examination aimed to identify and eliminate outliers using a local outlier factor (with parameters set at a contamination rate of 10%, 20 neighbors, and the Euclidean metric) because of its potential impact on the accuracy of the learning model.
From the complete dataset consisting of 740 cases, we divided it into two subsets: a training set (comprising 80% of the data, with a total of 592 samples, where individuals with NSCNP (POWs) numbered 373 and those without NSCNP numbered 219) to construct our predictive models, and a test set (representing 20% of the data, totaling 148 samples, with 90 POWs having NSCNP and 58 POWs without NSCNP) for external validation to evaluate model performance. We employed six distinct ML algorithms: neural network, random forest, logistic regression, gradient boosting, decision tree, and support vector machine. These algorithms were trained using a 10-fold cross-validation approach in the training set.
The primary measure of model performance focused on the calculation of the area under the curve (AUC), which was determined for both the training and test datasets, with emphasis on the target class being the average across all classes. Additionally, secondary indicators of model performance encompassed classification accuracy, recall, precision, and F1 score (which harmoniously combines recall and precision) for both the training and test data, with the same target class being the average across all classes. We categorized the predictive model's performance as excellent (AUC≥0.9), good (AUC between 0.8 and 0.9), fair (AUC between 0.7 and 0.8), or poor (AUC<0.7) based on the AUC value.13
We calculated the importance of feature permutation using the training data to determine the significance of each predictive variable. This analysis involved evaluating the contribution of each feature to the model’s performance by measuring its impact on the AUC, and consequently, any increase in the model's prediction error.
RESULTS
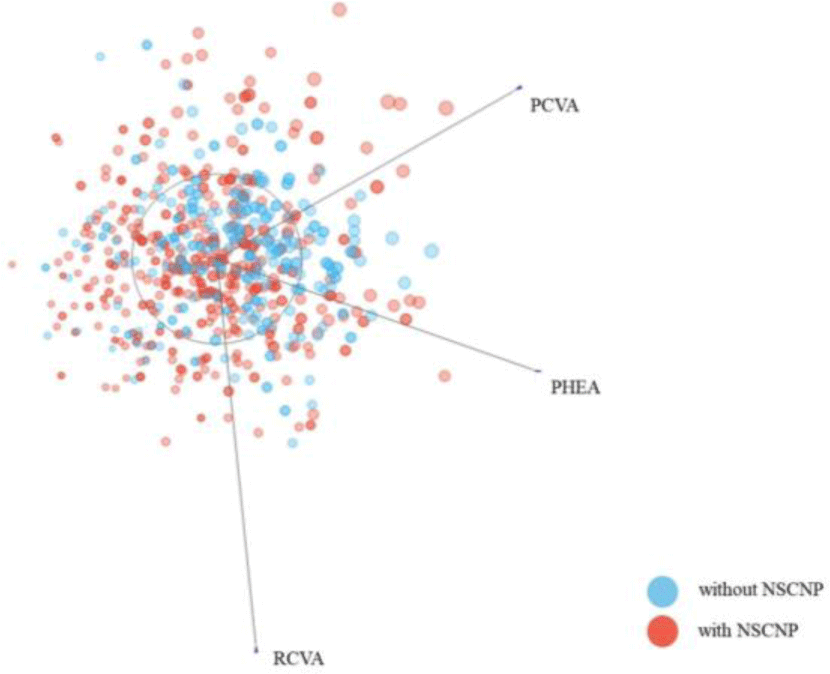
A total of 740 POWs (99 men and 641 women) were included in the ML analysis, with a NSCNP proportion of 62.6% (n=463, men=37, women=426). Means and standard deviations of NRS was 5.9±2.8 and 0.6±1.1 in POWs with and without NSCNP, respectively. The means and standard deviations of all variables are provided in Table 1. Figure 2 shows the distribution of RCVA, PCVA and PHEA data between POWs with and without NSCNP.
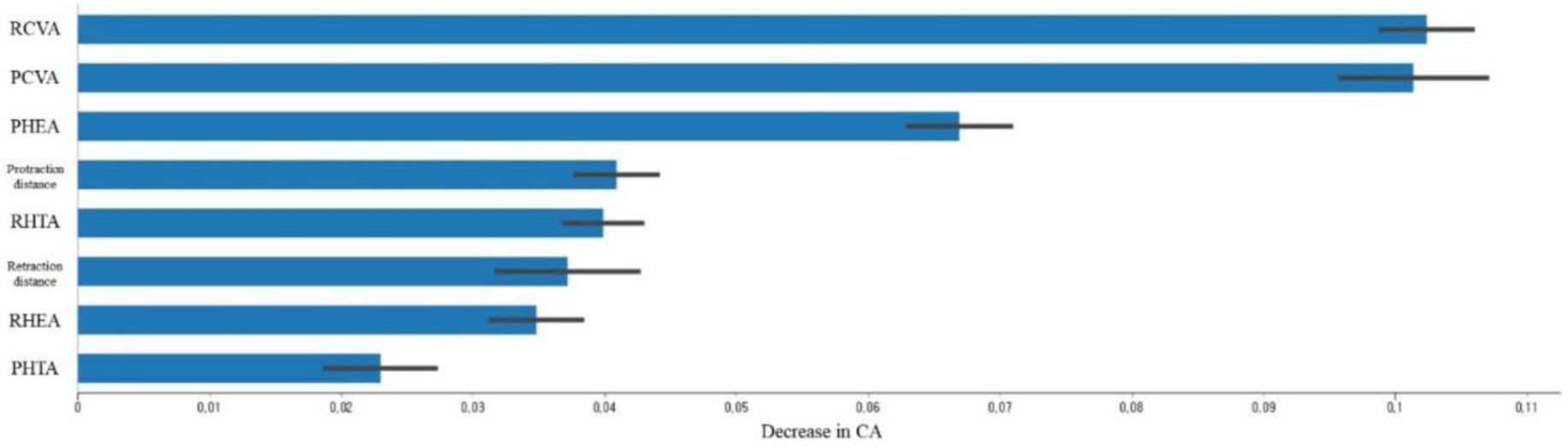
The performance of the six ML models for predicting the NSCNP during model training and testing is shown in Table 2, and the most important predictors of the best performance (random forest model) are described in Figure 3.
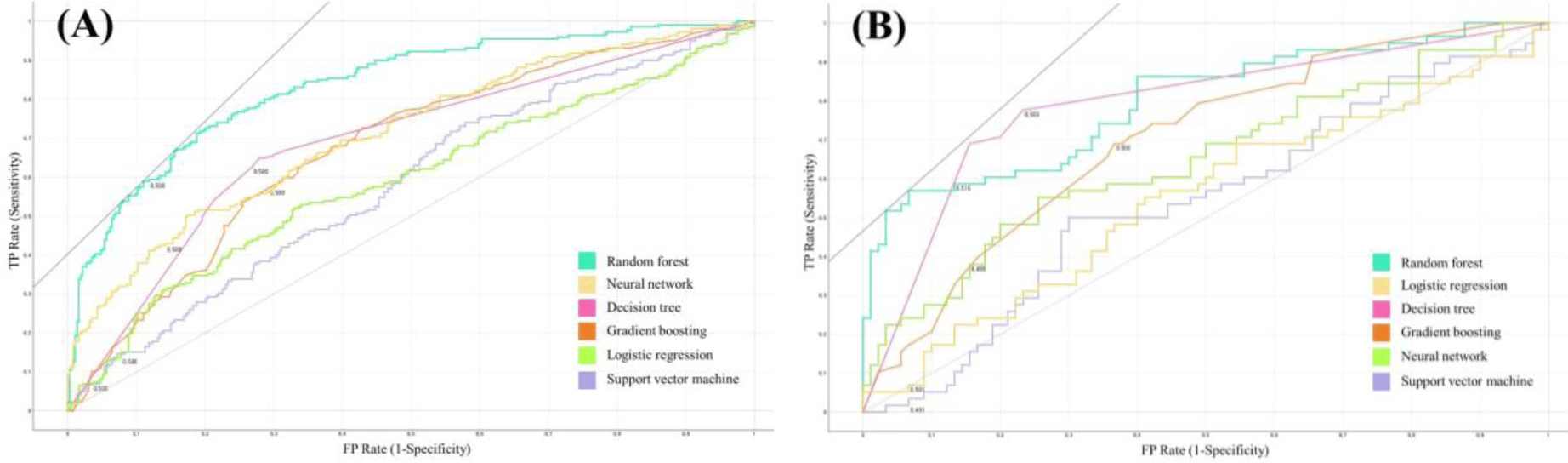
Six ML models in the training dataset classified POWs with and without NSCNP, performed in the order of high AUC, random forest (AUC,0.835 [good]; F1, 0.767; accuracy, 0.774), neural network (AUC, 0.711 [fair]; F1, 0.682; accuracy, 0.699], decision tree (AUC, 0.691 [poor]; F1, 0.695; accuracy, 0.693), gradient boosting (AUC, 0.676 [poor]; F1, 0.659; accuracy, 0.657), logistic regression (AUC, 0.590 [poor]; F1, 0.559; accuracy, 0.633), and support vector machine (AUC, 0.582 [poor]; F1, 0.589; accuracy, 0.593) (Table 2 and Figure 4). In the test dataset classification of POWs with and without NSCNP, six ML prediction models were performed in the following order: high AUC, random forest (AUC, 0.800 [good]; F1, 0.744; accuracy, 0.750), decision tree (AUC, 0.790 [fair]; F1, 0.772; accuracy, 0.770), gradient boosting (AUC, 0.701 [fair]; F1, 0.659; accuracy, 0.655), neural network (AUC, 0.649 [poor]; F1, 0.632; accuracy, 0.655), logistic regression (AUC, 0.548 [poor]; F1, 0.494; accuracy, 0.595), and support vector machine (AUC, 0.542 [poor]; F1, 0.506; accuracy, 0.568) (Table 2 and Figure 4).
For feature permutation importance, in the order of high impact AUC, RCVA, PCVA, PHEA, protraction distance, RHTA, retraction distance, RHEA, and PHTA (Figure 3).
DISCUSSION
This study represents a significant contribution to our understanding of NSCNP by investigating the relationship between cervical movements during protraction and retraction and the presence of NSCNP as well as by using ML models to classify individuals with and without NSCNP based on these kinematic variables. The findings of this study shed light on the intricate relationship between cervical movements and NSCNP. Traditionally, neck pain research has focused on association between neck posture and NSCNP or the linear relationship between neck pain and movement patterns and has often yielded inconsistent results. In this study, the authors recognized the potential for nonlinear relationships and employed ML techniques to capture these complex associations. The results indicate that the relationship between cervical movements and NSCNP is not straightforward, as evidenced by the variable perfor-mance of the ML models.
Six ML algorithms, including random forest, neural network, decision tree, gradient boosting, logistic regression, and support vector machine, were used to classify individuals with and without NSCNP. Random forest emerged as the top-performing model, demonstrating good accuracy and an AUC of 0.800 in the test dataset. Although direct comparison is difficult and related studies are lacking, in a study that classified individuals with and without neck pain using upper cervical rotation movement control test data, the AUC was 0.61, which was relatively lower than our study.20 The performance of this model indicates its potential utility in clinical settings for classifying individuals with NSCNP based on cervical movements during protraction and retraction. Although the decision tree model demonstrated fair performance, it also showed promise in classifying NSCNP cases, achieving an AUC of 0.790 in the test dataset. Gradient boosting, neural networks, and logistic regression, while showing lower AUC values, still had some predictive capabilities. However, the support vector machine model exhibited the lowest performance among ML algorithms.
In terms of feature permutation importance, the random forest model highlighted RCVA, PCVA, and PHEA as significant predictors of NSCNP. Nevertheless, except for PCVA and PHEA, there were no statistically discernible distinctions between individuals with and without NSCNP concerning the remaining influential predictors. Specifically, the disparity in PCVA and PHEA between individuals with and without NSCNP was only 1.58° and 1.92°, respectively. Previous studies have reported that women with neck pain exhibit a horizontal axis displacement of 10 cm for protraction and retraction distances, which is significantly smaller than that observed in asymptomatic women (6.8 cm).3 Another study also reported that the subclinical neck pain group displayed a greater displacement in the horizontal axis for retraction distance compared to the normal group.4 However, decreased cervical retraction might be attributed to factors such as sternocleidomastoid and posterior neck muscle tightness, limited cervical spine gliding, and weakened deep neck flexors responsible for cervical stabilization.21,22 Consequently, numerous physical therapists and various clinicians have endeavored to evaluate cervical retraction or craniocervical flexion movements, along with upper cervical motor control, in individuals with NSCNP.23-26
Similar to how clinicians assess these movements, the ML model also underscored the importance of RCVA in relation to cervical retraction as a significant predictor of NSCNP in the random forest model. Intriguingly, predictors associated with cervical protraction have also emerged as vital contributors to ML models. Therefore, further investigation is warranted to delineate the movement patterns of cervical protraction and retraction in individuals with NSCNP and to compare these patterns in individuals with and without NSCNP. Additionally, it is imperative to demonstrate the potential improvement in neck pain through interventions aimed at restoring normal movement patterns in individuals with NSCNP. The findings of this study have several implications for clinical practice and research. First, they emphasized the need to consider nonlinear relationships when studying NSCNP and other musculoskeletal conditions. ML techniques, as demonstrated here, offer a valuable tool for capturing such complexities. Second, the identification of key cervical kinematic variables such as RCVA, PCVA, and PHEA provides clinicians with potential targets for assessment and intervention in individuals with NSCNP. By monitoring and addressing abnormalities in these kinematic parameters, healthcare providers may be able to better diagnose and treat NSCNP. Third, the strong performance of the random forest model suggests its potential as a clinical tool for classifying NSCNP cases based on cervical movement. This could streamline the diagnostic process and assist treatment planning.
It’s important to acknowledge some limitations of this study. Because we did not control compensatory upper thoracic motion, cervical kinematics during protraction and retraction movements would be overestimated. Controlling compensatory motion data could enhance machine learning-based classification. The sample consisted primarily of office workers, which may limit the generalizability of the findings to other populations. Additionally, the retrospective design of the study using existing data may introduce selection bias and confounding variables. Future research in this area could focus on prospective studies with more diverse populations and consider additional clinical variables. Further investigation into the mechanisms underlying the relationship between cervical movements and NSCNP is warranted.
CONCLUSIONS
In conclusion, this study highlights the potential of ML models to enhance our understanding of NSCNP and offers valuable insights into the complex relationship between cervical movements during protraction and retraction and the presence of NSCNP. Cervical kinematic variables such as RCVA, PCVA and PHEA can be potential targets for assessment and intervention in individuals with NSCNP. Clinicians and researchers can leverage these findings to develop more effective diagnostic and treatment strategies for individuals with NSCNP.







